Lifestyle Khazanah Profil Baru Dram Lists Ensiklopedia
Technopedia Center
PMB University Brochure
Faculty of Engineering and Computer Science
S1 Informatics S1 Information Systems S1 Information Technology S1 Computer Engineering S1 Electrical Engineering S1 Civil Engineering

faculty of Economics and Business
S1 Management S1 Accountancy

Faculty of Letters and Educational Sciences
S1 English literature S1 English language education S1 Mathematics education S1 Sports Education
teknopedia

teknopedia

teknopedia

teknopedia

teknopedia

teknopedia
teknopedia
teknopedia
teknopedia
teknopedia
teknopedia
url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url url
  2. Weltenzyklopädie
  3. پویایی‌شناسی سیستم‌ها - ویکی‌پدیا، دانشنامهٔ آزاد
پویایی‌شناسی سیستم‌ها - ویکی‌پدیا، دانشنامهٔ آزاد
از ویکی‌پدیا، دانشنامهٔ آزاد
کالای پویا و نمودار گردشی پذیرش محصول جدید (مدل از مقالهٔ جان استرمن ۲۰۰۱)

پویایی‌شناسی سامانه‌ها یا دینامیک سامانه‌ها (به انگلیسی: System dynamics)، روشی برای درک رفتارهای یک سامانهٔ پیچیده در طول زمان است. در این روش با تمرکز بر حلقه‌های بازخورد (Feedback Loops) درون سامانه، تأثیرات غیرخطی و تاخیرهای زمانی در میان متغیرها و همچنین ماهیت انباشتی یا جریانی متغیرها به بررسی رفتار یک سامانه می‌پردازند. با توجه به ماهیت عددی روش پویایی‌های سامانه، این امکان وجود دارد که مدل‌های مبتنی بر این روش را با استفاده بهینه از رایانه شبیه‌سازی کرد و با مجموعه پارامترها و متغیرهای مختلف وضعیت سامانه برای یک بازه زمانی در آینده را پیش‌بینی نمود.

بررسی اجمالی

پویایی‌های سامانه با حلقه‌های بازخورد و تأخیرهای زمانی سروکار دارد که رفتار کل سامانه را مورد تأثیر قرار می‌دهند. چیزی که استفاده از پویایی‌های سامانه را از دیگر رویکردهای مطالعهٔ سامانه‌های پیچیده متمایز می‌سازد استفاده از حلقه‌های بازخورد و انباشت و جریان است. این عناصر به شرح چگونگی نمایش تأثیرات غیر خطی در سامانه‌های بظاهر ساده کمک می‌کنند.

پویایی‌های سامانه یک روش‌شناسی و روش مدل‌سازی ریاضی برای چارچوب‌بندی، درک، و بحث پیرامون موضوعات و مسائل پیچیده است. در حالیکه در دههٔ ۱۹۵۰ برای کمک به مدیران شرکت‌ها بمنظور بهبود درکشان از فرایندهای صنعتی ایجاد شد، در حال حاضر پویایی‌های سامانه در تمام بخش عمومی و خصوصی بمنظور طراحی و آنالیز سیاست‌ها بکار می‌رود.

در دههٔ ۱۹۹۰ نرم‌افزار مناسب پویایی‌های سامانه در نسخه‌های کاربرپسند توسعه یافت و به سامانه‌های گوناگون اعمال شد. مدل‌های پویایی‌های سامانه، مشکل همزمانی (علت و معلول متقابل) را با بروزرسانی کلیهٔ متغیرها در افزایش‌های زمانی کوچک با بازخوردهای مثبت و منفی و تأخیرهای زمانی برای ساختاربندی تعاملات و کنترل، حل می‌کنند. احتمالاً بهترین مدل شناخته‌شدهٔ پویایی‌های سامانه مربوط به کتاب «محدودیت‌های رشد»[۱] چاپ ۱۹۷۲ باشد. این مدل پیش‌بینی می‌کند که رشد تصاعدی منجر به فروپاشی اقتصادی در سدهٔ ۲۱ میلادی تحت طیف گسترده‌ای از سناریوهای رشد شود.

پویایی‌های سامانه جنبه‌ای از نظریهٔ سامانه‌ها به عنوان روشی برای درک رفتار پویای سامانه‌های پیچیده است. اساس روش، درک این مسئله است که ساختار هر سامانه — با روابط دایره‌ای، به‌هم‌پیوسته، و گاهی با تأخیر زمانی بین اجزایشان — اغلب به همان اندازه‌ای در تعیین رفتار اهمیت دارد که خود اجزاء به صورت منفرد. مثال‌هایش نظریه آشوب و پویایی اجتماعی است. همچنین ادعا شده که اغلب به دلیل وجود خواص کلی‌ای که نمی‌توان آن‌ها را در خواص اجزاء یافت، در برخی موارد نمی‌توان به توضیح رفتار کل در قالب رفتار اجزاء پرداخت.

تاریخچه

روش پویایی‌های سامانه در اواخر دههٔ پنجاه میلادی توسط جی فارستر در دانشگاه MIT بنیان نهاده شد. جی فاستر که همچنین به عنوان مخترع حافظهٔ مغناطیسی نیز شهرت دارد بعد از جابه‌جایی به دانشکدهٔ مدیریت Sloan همین دانشگاه روش داینامیک سامانه را برای سامانه‌های مختلف از جمله سامانه‌های اقتصادی و اجتماعی به کار برد. اولین مقالهٔ منتشر شده از جانب وی با این مضمون مربوط به مقاله‌ای است که در سال ۱۹۵۶ در مجله Harvard Business Review و با عنوان پویایی‌های صنعتی منتشر شد.

موضوعات پویایی‌های سامانه

عناصر نمودارهای پویایی‌های سامانه، بازخورد، انباشتگی جریان‌ها در انباشت‌ها و تأخیرهای زمانی هستند.

بعنوان تصویری از نحوهٔ استفاده از پویایی‌های سامانه، سازمانی را در نظر بگیرید که برای معرفی یک محصول مصرفی بادوام جدید نوآورانه برنامه‌ریزی می‌کند. چنین سازمانی به‌منظور طراحی برنامه‌های بازاریابی و تولید، به درک پویایی‌های ممکن بازار نیاز دارد.

نمودارهای حلقهٔ علیتی

در روش‌شناسی پویایی‌های سامانه، یک مسئله یا یک سامانه (مثلاً بوم‌سازگان، سامانه سیاسی، سامانه اقتصادی یا سامانه مکانیکی) نخست به عنوان نمودار حلقهٔ علیتی(حلقه علت و معلول) نمایش داده می‌شود. یک نمودار حلقهٔ علیتی نقشهٔ ساده‌ای از یک سامانه، همراه با همهٔ اجزای تشکیل‌دهنده و برهم‌کنش‌های آن‌هاست. با ضبط برهم‌کنش‌ها و در نتیجه حلقه‌های بازخورد (شکل زیر را ببینید)، یک نمودار حلقهٔ علیتی، ساختار یک سامانه را نشان می‌دهد. با درک ساختار یک سامانه، امکان تعیین رفتار یک سامانه در طول یک دورهٔ زمانی مشخص امکان‌پذیر می‌شود.

روابط علت و معلولی مربوط به بخش پول و سطح قیمت‌ها

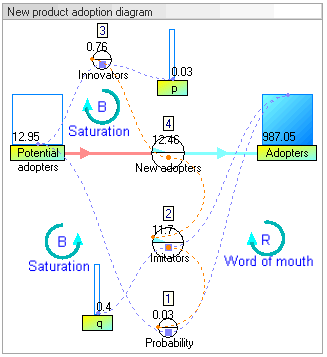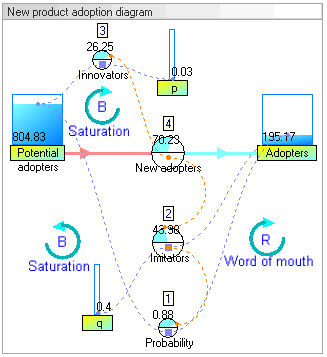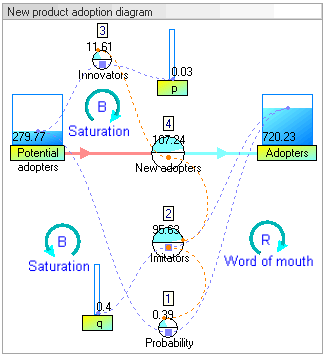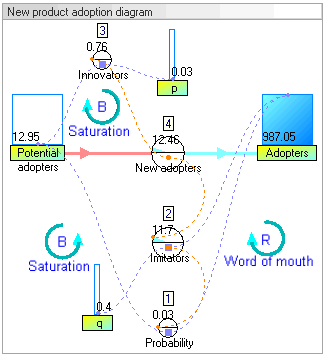
نمودار حلقهٔ علیتی مربوط به معرفی یک محصول جدید می‌تواند به این شکل باشد:

نمودار حلقهٔ علیتی مربوط به بکارگیری محصول جدید

در این نمودار دو حلقهٔ بازخورد وجود دارد. حلقهٔ تقویت مثبت (که با R برچسب‌زده شده) در سمت راست که نشان می‌دهد هرچه افراد بیشتری در حال حاضر محصول جدید را به‌کار گرفته‌اند، تأثیر حرف دهان قوی‌تر بوده‌است. همچنین ارجاعات بیشتر به محصول، بازنمود بیشتر، و اظهار نظرهای بیشتری وجود خواهد داشت. این بازخورد مثبت باید فروشی ایجاد کند که به رشد ادامه دهد.

حلقهٔ بازخورد دوم در سمت چپ، تقویت منفی (که با B برچسب‌زده شده) است. روشن است که رشد نمی‌تواند تا ابد ادامه پیدا کند، چون همچنان که افراد بیشتر و بیشتری به‌کار می‌گیرند، آنگاه به‌کارگیرندگان بالقوهٔ کمتر و کمتری باقی خواهند ماند.

هر دوی حلقه‌های بازخورد به‌طور هم‌زمان عمل می‌کنند، اما در زمان‌های متفاوت می‌توانند مقاومت‌های متفاوتی داشته باشند. بنابر این می‌توان انتظار رشد فروش در سال‌های اولیه و کاهش فروش در سال‌های بعد را داشت.

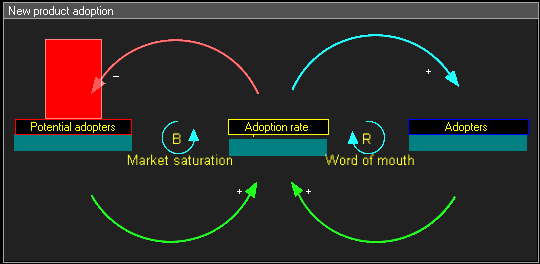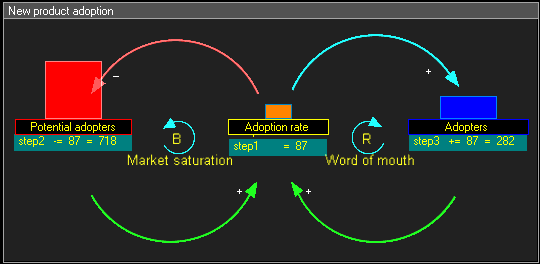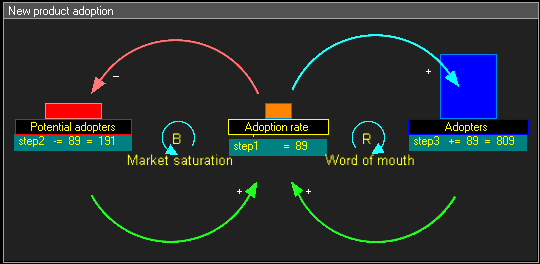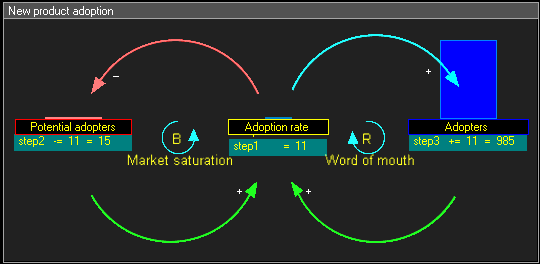
نمودار حلقهٔ علیتی مربوط به بکارگیری محصول جدید همراه با مقادیر گره‌ها پس از حسابان

در این نمودار حلقهٔ علیتی پویا باید به موارد زیر توجه داشت:

  • مرحله ۱: (+) پیکان‌های سبز نشان می‌دهند که نرخ به‌کارگیری تابعی از به‌کارگیرندگان بالقوه و به‌کارگیرندگان است.
  • مرحله ۲: (-) پیکان قرمز نشان می‌دهد که به‌کارگیرندگان بالقوه با نرخ به‌کارگیری کاهش پیدا می‌کنند
  • مرحله ۳: (+) پیکان آبی نشان می‌دهد که به‌کارگیرندگان با نرخ به‌کارگیرندی افزایش پیدا می‌کنند

نمودارهای بلوکی و نظریه کنترل

نمودارهای بلوکی روشی بسیار مفید و کارساز برای نمایش روابط پیچیده ذاتی در بسیاری از سیستم ها و مدل های سیستم در طول زمان است. نمادها در این نمودارها معنای دقیقی از نظر ریاضی دارند، بلوک ها بیانگر فرآیندها و پیکان های وارد شونده و خارج شونده از یک بلوک به ترتیب نشان دهنده، ورودی‌ها(محرک ها) و خروجی‌ها(پاسخ ها) هستند. یک پیکان بیانگر یک متغیر منفرد و علامت دو پیکان نشان‌دهنده‌ متغیرهای چندگانه است.

در شکل بالا یک نمودار بلوکی فرآیند مدیریت انبار را مشاهده می کنید که میتوان با استفاده از تاخیر مدت تحویل، تابع تبدیل میزان مطلوب موجودی انبار(ورودی) به میزان واقعی موجودی انبار(خروجی) را بدست آورد.

تابع تبدیل، نمایش ریاضی رابطه میان ورودی و خروجی یک سیستم خطی است و برای سیستم های پیوسته‌ با تبدیل لاپلاس و سیستم های گسسته با تبدیل پالس یا تبدیل زِد انجام می شود.

مفهوم حلقهٔ پس‌خور برای کنترل رفتار دینامیکی سامانه: این یک پس‌خور منفی است زیرا مقدار حس‌شده از مقدار فرمان (دلخواه) کم‌شده‌است تا سیگنال خطا که توسط کنترل‌کننده تقویت شده‌است شکل گیرد.

نمودارهای رَوَندنما یا فلوچارت

رَوَندنما یا فلوچارت (Flowchart) نوعی نمودار است که گردش کار یا فرایند انجام کاری را نمایش می‌دهد.

با مروری بر فلوچارت، روند اجرای عملیات، مراحل و جزئیات برنامه و ورودی و خروجی هر مرحله از برنامه مشخص می‌شود. استفاده از فلوچارت جهت حل هر مسئله‌ای مفید است و بدون در نظر گرفتن زبان برنامه‌نویسی، نوشتن برنامه را سهولت می‌بخشد. علاوه بر این فلوچارت جزئی باارزش از مستندات هر برنامه می‌باشد که با کمک آن تفسیر برنامه، عیب‌یابی و استفاده توسط شخصی به جز برنامه‌نویس را آسان می‌کند. برای رسم فلوچارت آگاهی و تسلط بر مراحل مورد نیاز و ترتیب آنها جهت به‌دست آوردن نتیجه مورد نظر با استفاده از داده‌های ورودی به الگوریتمی که فلوچارت برای آن کشیده می‌شود، لازم است.

رَوَندنما Flowchart

برنامه و نرم‌افزارهای کاربردی

نرم‌افزارها در این زمینه بیشتر در شاخه نرم‌افزارهای شبیه سازی (simulation software) قرار می‌گیرند . نرم‌افزارهای شبیه سازی مبتنی بر فرآیند مدل سازی یک پدیده واقعی با مجموعه ای از فرمول های ریاضی است. این اساساً برنامه ای است که به کاربر اجازه می دهد تا یک عملیات،فرآیند یا یک سیستم را از طریق شبیه سازی بدون انجام واقعی آن عملیات مشاهده کند روندها و تأثیرات را محاسبه و شبیه‌سازی کند. نرم افزار شبیه سازی به طور گسترده ای برای طراحی تجهیزات مورد استفاده قرار می گیرد تا محصول نهایی تا حد امکان به مشخصات طراحی نزدیک باشد بدون اینکه در فرآیند تغییرات هزینه بر باشد. نرم‌افزار شبیه‌سازی با پاسخ‌دهی بلادرنگ اغلب در بازی استفاده می‌شود، اما کاربردهای صنعتی مهمی نیز دارد. هنگامی که جریمه عملکرد نامناسب پرهزینه است، مانند خلبانان هواپیما، اپراتورهای نیروگاه هسته‌ای، یا اپراتورهای نیروگاه‌های شیمیایی، نمونه‌ای از پنل کنترل واقعی به شبیه‌سازی بلادرنگ پاسخ فیزیکی متصل می‌شود و تجربه آموزشی ارزشمندی را بدون ترس از یک نتیجه فاجعه بار ارائه می‌کند.


۱. نرم افزار ونسیم (VENSIM)

۲. نرم افزار Stella Architect که به اسم iThink هم شناخته می شود و توسط شرکت isee systems ساخته شده است

۳.ابزار سیمیولینک یک ابزار شبیه‌سازی همراه با نرم‌ افزار متلب است.

۴.ابزار Stateflow در نرم افزار متلب

۵.نرم افزار Flowgorithm برای رسم نمودارهای رَوَند نما

۶.نرم افزار Analytica که یک نرم افزار بصری است که توسط Lumina Decision Systems برای ایجاد، تجزیه و تحلیل و برقراری ارتباط مدل های تصمیم گیری کمی توسعه یافته است. که شامل سلسه مراتب دیاگرام های نفوذی برای ایجاد فضای بصری و مشاهده مدل ها، آرایه های هوشمند برای کار با داده های چند بعدی، شبیه سازی مونت کارلو برای تجزیه و تحلیل ریسک و عدم قطعیت، و بهینه سازی، از جمله برنامه ریزی خطی و غیرخطی را ترکیب می کند. طراحی آن، به ویژه نمودارهای تأثیرگذاری آن و درمان عدم قطعیت، بر اساس ایده هایی از حوزه تحلیل تصمیم است.

۷.نرم افزار DRAKON

منابع

پانویس

  1. ↑ The Limits to Growth
  2. ↑ «سیستم‌های پویا: اصول و تعیین هویت». بایگانی‌شده از اصلی در ۲۸ ژوئن ۲۰۱۲. دریافت‌شده در ۵ ژانویه ۲۰۱۲.
  3. ↑ System Dynamics: Principles and Identification
Pusat Layanan

UNIVERSITAS TEKNOKRAT INDONESIA | ASEAN's Best Private University
Jl. ZA. Pagar Alam No.9 -11, Labuhan Ratu, Kec. Kedaton, Kota Bandar Lampung, Lampung 35132
Phone: (0721) 702022
Email: pmb@teknokrat.ac.id