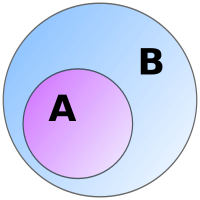
در ریاضیات، مجموعه ای چون A را زیرمجموعه B نامند هرگاه تمام اعضای A، اعضایی از B نیز باشند؛ در این حالت میگویند A زیر مجموعه B است. ممکن است هردوی A و B برابر باشند؛ در صورت نابرابریشان، گویند A زیرمجموعه سره ای از B است. رابطه زیرمجموعه بودن را شمول مینامند. «A زیرمجموعه B» را میتوان به صورت «B شامل A» یا «B مجموعه A را در بر میگیرد» یا «A مشمول در B است» نیز بیان کرد.
روابط زیرمجموعگی روی مجموعهها، رابطه ترتیب جزئی را رویشان تعریف میکند. در حقیقت، زیرمجموعههای یک مجموعه دلخواه، تحت رابطه زیرمجموعگی تشکیل جبر بولی میدهند که در آن جوین و میت همان اشتراک و اجتماع اند و خود رابطه زیرمجموعه بودن را رابطه شمول بولی مینامند.
تعریف
اگر و دو مجموعه باشند و تمام اعضای در نیز باشد، آنگاه:
- میتوان گفت که زیرمجموعهٔ است. و آن را به صورت میتوانیم بنویسیم.
همچنین از سوی دیگر میتوان گفت:
- B زیرمجموعهٔ A است.
به عنوان مثال، اگر داشته باشیم
- آنگاه که با حذف عضوهای ۲ و ۳ بهدست آمده است را زیرمجموعهٔ B میگویند.
اگر مجموعهٔ A زیرمجموعهٔ B باشد و همزمان مجموعهٔ B نیز زیرمجموعهٔ A، مجموعههای A و B با یکدیگر برابرند.
زیر مجموعه محض (سره)
اگرA B، ولی A≠ B آنگاه A زیر مجموعه محض یا سره Bنامیده میشود
همه زیر مجموعههای یک مجموعه به جز خود مجموعه را زیر مجموعههای محض یا سره میگویند.
به عنوان مثال ، و باشد آنگاه A زیر مجموعه محض (سره) مجموعه B میباشد.
توجه داشته باشید هر مجموعه (تهی) را به عنوان زیر مجموعه سره خود دارد اما خود (تهی) زیر مجموعه سره ندارد.
تعداد زیر مجموعههای یک مجموعه
تعداد زیر مجموعههای یک مجموعه n عضوی برابر است با .
تعداد زیر مجموعههای محض (سره) یک مجموعه n عضوی برابر است با .
منابع
- مشارکتکنندگان ویکیپدیا. «Subset». در دانشنامهٔ ویکیپدیای انگلیسی، بازبینیشده در ۲۴ آوریل ۲۰۲۱.
کتابشناسی
- Jech, Thomas (2002). Set Theory. Springer-Verlag. ISBN 3-540-44085-2.




















