جستجوی بازه‌ای

جستجوی بازه‌ای در ساختمان داده‌ها، شامل پیش‌پردازش مجموعهٔ S از اشیا است تا مشخص شود کدام یک از اشیای S با بازهٔ مدنظر که شیء سؤال نیز نامیده می‌شود، تقاطع دارند. به عنوان مثال، اگر S، مجموعه‌ای از نقاط باشد که هریک متناظر با مختصات یک شهر است، یک نوع مسئلهٔ هندسی مورد نظر، یافتن شهرهایی که در محدودهٔ طول و عرض جغرافیایی داده شده واقع‌اند، می‌باشد.

مسئلهٔ جستجوی بازه‌ای و داده ساختارهایی که آن را حل می‌کنند، مسئله‌ای اساسی در هندسه محاسباتی است. این مسئله در حوزه‌هایی مانند سیستم‌های اطلاعات جغرافیایی (GIS)، طراحی به کمک کامپیوتر (CAD) و پایگاه داده‌ها کاربرد دارد.

انواع

صورت‌های گوناگونی از این مسئله وجود دارد که به تبع آن داده ساختارهای گوناگونی مورد استفاده قرار داده می‌گیرند.^[۱] برای داشتن راه‌حل بهینه، موارد مختلفی باید مدنظر قرار داده شوند از جمله:

نوع اشیای مورد جستجو: الگوریتم‌ها بر اساس نوع اشیای مورد بررسی انتخاب می‌شوند، برای مثال می‌توان نقاط، خطوط، چندضلعی‌ها را مورد بررسی قرار داد. ساده‌ترین اشیا نیز نقاط هستند که بیشتر از سایر اشیاء مورد بررسی قرار گرفته‌اند.
نوع بازه: بازهٔ مورد بررسی باید برای یک مجموعهٔ از پیش تعیین شده مشخص گردد. بازه‌هایی که تاکنون بیشتر مورد بررسی قرار گرفته‌اند و مسائل حل شده با آن‌ها مستطیل‌های محوری (جستجوی بازه‌ای قائم)، کره‌ها و دایرهها، نیم‌فاصلهله‌ها هستند.
سؤال مطرح شده: اگر بخواهیم لیست اشیایی را که مجدودهٔ سؤالات را تقسیم می‌کنند گزارش کنیم، آنگاه مسئله تبدیل به یک گزارش بازه‌ای خواهد شد. اگر بخواهیم تنها تعداد اشیایی که با بازه تقاطع دارند را بررسی کنیم، آنگاه با مسئلهٔ شمارش بازه‌ای مواجه‌ایم.
تفاوت جستجوی بازه‌ای پویا با جستجوی بازه‌ای ایستا: در حالت ایستا، مجموعهٔ S، از ابتدا مشخص است و تا پایان تغییری نمی‌کند. در حالت پویا، اشیای جدیدی اضافه یا اشیای قبلی حذف می‌شوند.
مفهوم جستجوی بازه‌ای آفلاین: هم مجموعهٔ اشیا و هم مجموعهٔ سؤالات از ابتدا مشخص هستند.

داده ساختارها

جستجوی بازه‌ای قائم

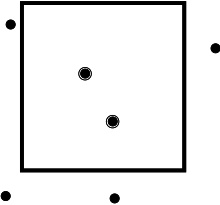
در جستجوی بازه‌ای قائم، مجموعهٔ S از n نقطه و d بُعد تشکیل شده‌است و مجموعهٔ مورد پرسش، بازه‌هایی در این ابعاد است؛ بنابراین مجموعهٔ مورد پرسش از مستطیل‌های محوری چندبعدی تشکیل شده‌است. اگر اندازهٔ خروجی را k در نظر بگیریم، جان بنتلی با استفاده از یک درخت کی‌دی توانست در زمان ${\displaystyle O{\big (}n^{1-{\frac {1}{d}}}+k{\big )}}$ (پیچیدگی زمانی) و با حافظهٔ ${\displaystyle O(n)}$ این مسئله را حل کند.^[۲] همچنین بنتلی با استفاده از داده ساختار درخت بازه‌ای، توانست زمان مورد نیاز برای حل این مسئله را به ${\displaystyle O(\log ^{d}n+k)}$ برساند. البته در این حالت حافظهٔ مورد نیاز به ${\displaystyle O(n\log ^{d-1}n)}$ افزایش پیدا کرد.^[۳] دن ویلارد نیز با استفاده از داده ساختار دیگری توانست این مسئله را در زمان ${\displaystyle O(\log ^{d-1}n+k)}$ حل کند.

در حالی‌که در مدل ماشین اشاره‌گر نتایج بالا حاصل شده بودند، با تغییر مدل به مدل رَم، پیشرفت‌های بیشتری نیز حاصل شد. برنارد چازل توانست با استفاده از داده ساختاری به نام درخت بازه‌ای فشرده، در ${\displaystyle O(\log n)}$ و با حافظهٔ ${\displaystyle O(n)}$ مسئلهٔ شمارش بازه‌ها را حل کند. لازم است ذکر شود که کمی بعد، جوزف جاجا و دیگران توانستند این مسئله را در زمان بهتری نیز حل کنند.

تا سال ۲۰۱۵، بهترین الگوریتم‌ها توسط Timothy M. Chan ,Kasper Larsen و Mihai Pătrașcu ارائه شده‌اند که همگی نیز از داده ساختار درخت بازه‌ای فشرده و مدل رم استفاده می‌کنند که در این‌جا ذکر شده‌اند:

زمان ${\displaystyle O(\log \log n+k\log \log n)}$ ، حافظهٔ ${\displaystyle O(n\log \log n)}$
زمان ${\displaystyle O(\log ^{\epsilon }n+k\log ^{\epsilon }n)}$ ، حافظهٔ $O(n)$
زمان ${\displaystyle O(\log \log n+k)}$ ، حافظهٔ ${\displaystyle O(n\log ^{\epsilon }n)}$

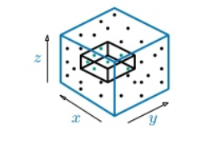
در حالت قائم، اگر بازه کراندار باشد، با یک مسئلهٔ چهاربعدی مواجه‌ایم. در صورتی که سر یا ته یکی از بازه‌ها بی‌نهایت باشد، مسئله سه‌بعدی خواهد بود و در صورتی که هر دوی آنها بی‌نهایت باشند، مسئله دوبعدی است.

جستجوی بازه‌ای پویا

در حالی‌که در جستجوی بازه‌ای ایستا مجموعهٔ S از پیش تعیین شده‌است، در جستجوی بازه‌ای پویا با حذف یا اضافه شدن نقاط مواجه می‌شویم. در نسخهٔ افزایشی این مسئله، تنها مجاز به افزودن اعضا هستیم. برعکس در نسخهٔ کاهش این مسئله تنها حذف اعضا مجاز است. هر دو نسخهٔ افزایشی و کاهشی در زمان ${\displaystyle O(\log n+k)}$ قابل حل هستند، اما هنوز مشخص نیست که آیا جستجوی بازه‌ای کلی را نیز می‌توان با این پیچیدگی زمانی حل کرد یا خیر.^[۴]

جستجوی بازه‌ای رنگی

مسئلهٔ جستجوی بازه‌ای رنگی زمانی مطرح می‌شود که نقاط داده شده دارای ویژگیهای قابل دسته‌بندی هستند. اگر برای هر دسته یک رنگ در نظر بگیریم، آنگاه صورت مسئله تبدیل به تعداد رنگ‌های موجود در آن بازه می‌شود. در سال ۱۹۹۵، Prosenjit Gupta و سایرین داده ساختاری را مطرح کردند که مسئلهٔ جستجوی بازه‌ای قائم در دو بعد را در زمان ${\displaystyle O(\log ^{2}n)}$ و با مصرف ${\displaystyle O(n^{2}\log ^{2}n)}$ حافظه حل کرد.

درخت جستجوی بازه‌ای یک بعدی

فرض کینم در بازه‌ [l,r] به دنبال برگ (راسی از درخت که فرزندی ندارد) با بیشترین مقدار در سمت راست و نیز در سمت چپ هستیم؛ برگ سمت راست را u و چپ را v می‌نامیم.تمام رئوس بین u و v در این بازه قرار میگیرند. اگر u برابر با l و v برابر با r باشد ، آنگاه آن راس و تمام زیر درختش را به بازه اضافه میکنیم (لازم است ذکر شود که درخت ما هریک از انواع درخت دودویی جستجوی متوازن مانند AVL tree و RedBlack tree میتواند باشد). بازه‌ی مورد نظر در زیردرخت [u,v] قرار میگیرد. برای توضیح بیشتر ، فرض کنیم در حال حاضر آخرین راسی که بررسی کرده‌ایم راس z است. اگر از z به سمت چپ بازه (به سمت u) حرکت کنیم ، زیردرخت فرزند چپ را به بازه‌ی کنونی اضافه میکنیم. بالعکس، اگر از z به سمت راست بازه (به سمت v) حرکت کنیم، زیردرخت فرزند چپ را به بازه‌ی کنونی میفزاییم. چون درخت ما یک درخت دودویی جستجوی متوازن است، این عملیات حداکثر به اندازه‌ ارتفاع درخت یعنی ${\displaystyle O(\log n)}$ به طول می‌انجامد.

کاربردها

جستجوی بازه‌ای و جستجوی بازه‌ای قائم، علاوه بر هندسهٔ محاسباتی، در سؤالات بازه‌ای خصوصاً در پایگاه‌های داده کاربردهای فراوانی دارند. جستجوی بازه‌ای رنگی نیز در مسائل مبتنی بر داده‌های دسته‌بندی‌شده به‌کار می‌رود. برای مثال مشخص کردن سطرهایی از پایگاه دادهٔ حساب‌های بانکی با جستجوی بازه‌ای مدل می‌شود و مشخص کردن سطرهایی از پایگاه دادهٔ حساب‌های بانکی که متعلق به افراد بین سنین ۲۰ تا ۳۰ است و موجودی حساب آنها بین ۱۰۰۰ تا ۲۰۰۰ دلار است، با جستجوی بازه‌ای رنگی دوبعدی مدل می‌شود که سن و موجودی حساب این دو بعد می‌باشند.

جستارهای وابسته

درخت بازه‌ها
درخت پاره‌خطی (cartesian tree)
درخت فنویک (fenwick tree)
k-d tree

منابع

↑ Agarwal, P. K. ; Erickson, J. (1999), in Chazelle, Bernard; Goodman, Jacob; Pollack, Richard (eds.), Advances in Discrete and Computational Geometry: proceedings of the 1996 AMS-IMS-SIAM joint summer research conference, Discrete and Computational Geometry--Ten Years Later, July 14-18, 1996, Mount Holyoke College, Contemporary Mathematics, 223, American Mathematical Society Press, pp. 1–56
↑ Bentley, Jon (1975). "Multidimensional binary search trees used for associative searching"
↑ Bentley, Jon (1980). "Multidimensional divide-and-conquer
↑ Willard, Dan (1985). "New data structures for orthogonal range queries". SIAM Journal on Computing

[1] Agarwal, P. K. ; Erickson, J. (1999), in Chazelle, Bernard; Goodman, Jacob; Pollack, Richard (eds.), Advances in Discrete and Computational Geometry: proceedings of the 1996 AMS-IMS-SIAM joint summer research conference, Discrete and Computational Geometry--Ten Years Later, July 14-18, 1996, Mount Holyoke College, Contemporary Mathematics, 223, American Mathematical Society Press, pp. 1–56

[2] Bentley, Jon (1975). "Multidimensional binary search trees used for associative searching"

[3] Bentley, Jon (1980). "Multidimensional divide-and-conquer

[4] Willard, Dan (1985). "New data structures for orthogonal range queries". SIAM Journal on Computing

[۱]

[۲]

[۳]

[۴]