
تحلیل مؤلفههای اصلی (به انگلیسی: Principal Component Analysis - PCA) تبدیلی در فضای برداری است، که تحلیل مجموعه دادههای بزرگ با تعداد زیادی بعد یا ویژگی، افزایش تفسیرپذیری دادهها با حفظ حداکثر مقدار اطلاعات و تجسم دادههای چند بعدی را فراهم میکند. تحلیل مؤلفههای اصلی در واقع، یک تکنیک آماری برای کاهش ابعاد یک مجموعه دادهاست. این کار با تبدیل خطی دادهها به یک سیستم مختصات جدید انجام میشود که (بیشتر) تغییرات در دادهها را میتوان با ابعاد کمتری نسبت به دادههای اولیه توصیف کرد. بسیاری از مطالعات از دو مؤلفه اصلی اول برای نمایش دادهها در دو بعد و شناسایی بصری خوشههای نقاط داده نزدیک به هم استفاده میکنند. تحلیل مؤلفههای اصلی در بسیاری از زمینهها مانند ژنتیک جمعیت، مطالعات میکروبیومها و علوم جوی کاربرد دارد.[۱]
مؤلفهها اصلیِ مجموعهای از نقاط در یک فضای مختصات حقیقی، دنبالهای از بردارهای واحد هستند، که در آن بردار -ام امتداد خطی است که بهترین تطابق را با دادهها دارد و در عین حال به بردار اول متعامد است. در اینجا بهترین خط، خطی است که میانگین مجذورات فاصله عمود نقاط از خط را کمینه میکند. این بردارها یک پایه متعامد و یکه را تشکیل میدهند که در آن ابعاد مختلف دادهها بهطور خطی همبستگی ندارند. تحلیل مؤلفههای اصلی فرایند محاسبه مؤلفههای اصلی و استفاده از آنها برای تغییر پایه دادهها است که گاهی فقط از چند مؤلفه اصلی اول استفاده میکند و بقیه را نادیده میگیرد.
تاریخچه
تحلیل مؤلفههای اصلی اولین بار در سال ۱۹۰۱ توسط کارل پیرسون[۲] به عنوان متناظری از قضیه محورهای اصلی در مکانیک ارائه شد. این روش بعدها به صورت مستقل توسط هارولد هتلینگ[۳] در دهه ۱۹۳۰ میلادی توسعه یافت و نامگذاری شد. باتوجه به کاربرد این روش آن را تبدیل گسسته کارانن-لوف یا KLT در پردازش سیگنال نیز یا تبدیل هتلینگ در کنترل کیفیت چند متغیره مینامند.
ایده
تحلیل مؤلفههای اصلی را میتوان به عنوان برازش یک بیضی با ابعاد به دادهها در نظر گرفت، که در آن هر محور بیضی یک مؤلفه اصلی را نشان میدهد. اگر برخی از محورهای بیضی کوچک باشد، واریانس در امتداد آن محور نیز کوچک است. برای پیدا کردن محورهای بیضی، ابتدا باید با کم کردن میانگین مقادیر هر متغیر از آنها، میانگین مجموعه داده را صفر کنیم. این مقادیر تبدیل شده حالا به جای مقادیر اصلی برای هر یک از متغیرها استفاده میشود. سپس، ماتریس کواریانس دادهها را محاسبه کرده و مقادیر ویژه و بردارهای ویژه آن را محاسبه میکنیم. سپس باید هر یک از بردارهای ویژه متعامد را نرمال کنیم تا آنها را به بردارهای واحد تبدیل کنیم. پس از انجام این کار، هر یک از بردارهای ویژه واحد متعامد را میتوان به عنوان محوری از بیضی برازش دادهها تفسیر کرد. این انتخاب پایه، ماتریس کوواریانس را به ماتریسی قطری تبدیل میکند، که در آن درایههای روی قطر واریانس هر محور را نشان میدهد. درصد واریانسی که هر بردار ویژه از اطلاعات موجود بیان میکند را میتوان با تقسیم مقدار ویژه مربوط به آن بردار ویژه بر مجموع همه مقادیر ویژه محاسبه کرد.
جزئیات
تحلیل مؤلفههای اصلی در تعریف ریاضی[۴] یک تبدیل خطی متعامد است که داده را به دستگاه مختصات جدید میبرد بهطوریکه بزرگترین واریانس داده بر روی اولین محور مختصات، دومین بزرگترین واریانس بر روی دومین محور مختصات قرار میگیرد و همینطور برای بقیه.
ماتریس داده با میانگین تجربی صفر، که هر سطر یک مجموعه مشاهده و هر ستون دادههای مربوط به یک شاخصه است را در نظر بگیرید. از منظر ریاضی، این تبدیل با مجموعهای تایی از بردارهای -بعدیِ وزن یا ضرایب تعریف میشود که هر بردار سطری از را به بردار جدیدی از امتیازات مؤلفههای اصلی به صورت
تطبیق میدهد. به این صورت که متغیرهای در بیشترین واریانس ممکن از دادههای را داشته باشد. همچنین هر بردار ضریب باید یک بردار واحد باشد و معمولاً بسیار کمتر از انتخاب میشود.
مؤلفه اول
برای اینکه واریانس را بیشینه کنیم، اولین بردار وزن باید شرط زیر را برآورده کند:
و اگر آن را به صورت ماتریسی بنویسیم خواهیم داشت:
از آنجایی که باید یک بردار واحد باشد خواهیم داشت:
کمیتی که باید بیشینه شود را میتوان به عنوان خارج قسمت رایلی در نظر گرفت. یک نتیجه برای یک ماتریس مثبت نیمه معین مانند این است که حداکثر مقدار ممکن ضریب، بزرگترین مقدار ویژه ماتریس است، که زمانی رخ میدهد که بردار ویژه مربوط باشد.
با پیدا کردن ، اولین مؤلفه اصلی بردار داده را میتوان به صورت امتیاز در مختصات تبدیلشده به دست آورد.
مؤلفههای بعدی
مؤلفه ام را میتوان با کم کردن مؤلفه اصلی اول از بهدستآورد:
و سپس بردار وزنی که حداکثر واریانس را از این ماتریس داده جدید استخراج میکند بهدست میآوریم:
عبارت بالا بردارهای ویژه باقیمانده را با حداکثر مقادیر برای کمیت در پرانتز با مقادیر ویژه متناظر آنها را بهدست میآورد؛ بنابراین بردارهای وزن همان بردارهای ویژه هستند. مؤلفه اصلی ام بردار داده را میتوان به صورت امتیاز در مختصات تبدیلشده به دست آورد.
بنابراین، تجزیه کامل مؤلفههای اصلی را میتوان به این صورت نشان داد:
که در آن یک ماتریس از وزنها است که ستونهای آن بردارهای ویژه هستند. ترانهاده گاهی تبدیل سفید یا کروی نامیده میشود.
تجزیه مقدارهای منفرد
تبدیل مؤلفههای اصلی را میتوان با تجزیه ماتریس دیگری، یعنی تجزیه مقدارهای منفرد انجام داد.
که اینجا یک ماتریس قطری از اعداد مثبت (یا همان مقادیر تکین ) است. یک ماتریس است که ستونهای آن بردارهای متعامد واحدی به طول هستند که بردارهای تکین چپ نامیده میشوند و یک ماتریس است که ستونهای آن بردارهای متعامد واحدی به طول هستند که بردارهای تکین راست نامیده میشوند.
با این تجزیه میتوان ماتریس را به صورت زیر نوشت:
که ماتریس قطری مربعی شامل مقادیر تکین است که صفرهای اضافی آن حذف شدهاست و عبارت برای آن برقرار است. مقایسه با بردارهای ویژه نشان میدهد که بردارهای تکین راست برابر با بردارهای ویژه و همچنین مقادیر تکین برابر با ریشه دوم مقادیر ویژه هستند. با استفاده از تجزیه مقدارهای منفرد، ماتریس امتیاز را به صورت زیر نوشت:
بنابراین هر ستون ماتریس را میتوان از حاصل ضرب بردارهای تکین چپ و مقدار تکین متناظر بهدستآورد.
محدودیتهای تحلیل مولفههای اصلی
استفاده از تحلیل مؤلفههای اصلی منوط به فرضهایی است که در نظر گرفته میشود. از جمله:
- فرض خطی بودن
فرض بر این است که مجموعه داده ترکیب خطی پایههایی خاص است.
- فرض بر این که میانگین و کواریانس از نظر احتمالاتی قابل اتکا هستند.
- فرض بر این که واریانس شاخصه اصلی دادهاست.
محاسبه مولفههای اصلی با استفاده از ماتریس کواریانس
بر اساس تعریف ارائه شده از تحلیل مؤلفههای اصلی، هدف از این تحلیل انتقال مجموعه داده X با ابعاد M به داده Y با ابعاد L است. بنابرین فرض بر این است که ماتریس X از بردارهای تشکیل شدهاست که هر کدام به صورت ستونی در ماتریس قرار داده شدهاست. بنابرین با توجه به ابعاد بردارها (M) ماتریس دادهها به صورت است.
محاسبه میانگین تجربی و نرمالسازی دادهها
نتیجه میانگین تجربی، برداری است که به صورت زیر به دست میآید:
که بهطور مشخص میانگین تجربی روی سطرهای ماتریس اعمال شدهاست.
سپس ماتریس فاصله تا میانگین به صورت زیر به دست میآید:
که h برداری با اندازه با مقدار ۱ در هرکدام از درایهها است.
محاسبه ماتریس کواریانس
ماتریس کواریانس C با ابعاد به صورت زیر به دست میآید:
- بهطوری که:
- میانگین حسابی است.
- ضرب خارجی است.
- ماتریس ترانهاده مزدوج ماتریس است.
محاسبه مقادیر ویژه ماتریس کواریانس و بازچینی بردارهای ویژه
در این مرحله، مقادیر ویژه و بردارهای ویژه ماتریس کواریانس، ، به دست میآید.
V ماتریس بردارهای ویژه و D ماتریس قطری است که درایههای قطر آن مقادیر ویژه هستند. آنچنان که مشخص است، هر مقدار ویژه متناظر با یک بردار ویژه است. به این معنا که ماتریس V ماتریسی است که ستونهای آن بردارهای ویژه میباشند و بردار ویژه در ستون qام قرار دارد و مقدار ویژه qام یعنی درایهٔ متناظر با آن است. بازچینی بردارهای ویژه بر اساس اندازهٔ مقادیر ویژه متناظر با آنها صورت میگیرد؛ یعنی بر اساس ترتیب کاهشی مقادیر ویژه، بردارهای ویژه بازچینی میشوند؛ یعنی
انتخاب زیرمجموعهای از بردارهای ویژه به عنوان پایه
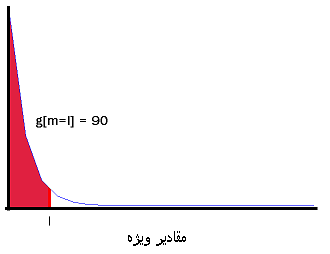
انتخاب زیرمجموعهای از بردارهای ویژه با تحلیل مقادیر ویژه صورت میگیرد. زیرمجموعه نهایی با توجه به بازچینی مرحله قبل به صورت انتخاب میشود. در اینجا میتوان از انرژی تجمعی استفاده کرد که طبق آن
انتخاب l باید به صورتی باشد که حداقل مقدار ممکن را داشته باشد و در عین حال g مقدار قابل قبولی داشته باشد. بهطور مثال میتوان حداقل l را انتخاب کرد که
بنابرین خواهیم داشت:
انتقال داده به فضای جدید
برای این کار ابتدا تبدیلات زیر انجام میگیرد: ماتریس انحراف معیار مجموعه دادهاست که میتواند به صورت زیر به دست بیاید:
سپس داده به صورت زیر تبدیل میشود:
که ماتریسهای و در بالا توضیح داده شدهاند. دادهها میتوانند به ترتیب زیر به فضای جدید برده شوند:
کاربرد
هوش
اولین کاربرد تحلیل مؤلفهای در پیداکردن و اندازهگیری مؤلفههای هوش انسانی بود. در گذشته باورها بر این بود که هوش دارای مؤلفههای نامرتبط مختلفی مانند هوش فضایی، هوش کلامی، استنتاج، قیاس و غیره است و میتوان امتیازات مربوط به این موارد را با تحلیل مؤلفهای از نتایج آزمونهای مختلف بهدستآورد تا یک شاخص واحد به نام ضریب هوش (IQ) بهدستآورد. روانشناس آماری چارلز اسپیرمن در واقع تحلیل مؤلفهای را در سال ۱۹۰۴ برای نظریه دو عاملی هوش خود توسعه داد و یک تکنیک رسمی را به علم روانسنجی اضافه کرد. در سال ۱۹۲۴، تورستون ۵۶ عامل هوش را بررسی کرد و مفهوم سن ذهنی را توسعه داد. تستهای استاندارد هوش امروزی بر اساس همین کار اولیه است.[۵]
ژنتیک جمعیت
در سال ۱۹۷۸ کاوالی-اسفورزا و دیگران پیشگام استفاده از تحلیل مؤلفههای اصلی برای خلاصهکردن دادهها دربارهٔ تنوع در فرکانسهای ژن انسانی در مناطق مختلف بودند. مؤلفهها، الگوهای متمایزی از جمله گرادیان و امواج سینوسی را نشان دادند. آنها این الگوها را ناشی از رویدادهای مهاجرت باستانی تفسیر کردند.
نرمافزارها
- در نرمافزار متلب تابع
princompمؤلفههای اصلی را بازمیگرداند که در نسخههای جدید، تابعpcaجایگزین آن شدهاست. - در زبان پایتون کتابخانه matplotlib دارای پکیج PCA در ماژول
mlab.است. - کتابخانه scikit-learn در پایتون برای یادگیری ماشین که شامل PCA, PCA احتمالی، Kernel PCA, Sparse PCA و تکنیکهای دیگر در ماژول
decompositionاست. - OpenCV
- Eviews
- در نرمافزار R تابع
prcompوprincompمؤلفههای اصلی را بازمیگرداند.prcompاز تجزیه مقدارهای منفرد استفاده میکند که بهطور کلی دقت عددی بهتری دارد. برخی از پکیجها که PCA را در R پیادهسازی میکنند، عبارتند از:ade4وveganوExPosition
جستارهای وابسته
- تحلیل مولفههای مستقل
- تحلیل تفکیک خطی
- تجزیه مقدارهای منفرد
- فشردهسازی دادهها
- تحلیل تناظر
- فاکتورگیری نامنفی ماتریس
- حداقل مربعات جزیی
منابع
- ↑ Jolliffe, Ian T.; Cadima, Jorge (2016-04-13). "Principal component analysis: a review and recent developments". Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences. 374 (2065): 20150202. doi:10.1098/rsta.2015.0202. PMC 4792409. PMID 26953178.
- ↑ Pearson, K. (1901). "On Lines and Planes of Closest Fit to Systems of Points in Space". Philosophical Magazine. 2 (11): 559–572. doi:10.1080/14786440109462720.
- ↑ Hotelling, H. (1933). Analysis of a complex of statistical variables into principal components. Journal of Educational Psychology, 24, 417–441, and 498–520.
Hotelling, H (1936). "Relations between two sets of variates". Biometrika. 28 (3/4): 321–377. doi:10.2307/2333955. JSTOR 2333955. - ↑ Jolliffe I.T. Principal Component Analysis بایگانیشده در ۱۶ اکتبر ۲۰۱۹ توسط Wayback Machine, Series: Springer Series in Statistics, 2nd ed. , Springer, NY, 2002, XXIX, 487 p. 28 illus. ISBN 978-0-387-95442-4
- ↑ Kaplan, R.M. , & Saccuzzo, D.P. (2010). Psychological Testing: Principles, Applications, and Issues. (8th ed.). Belmont, CA: Wadsworth, Cengage Learning.
















































![{\displaystyle u[m]={\frac {1}{N}}\sum _{i=1}^{N}{X[m,i]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37836d37aa0d3cce9b68dd60b5c213d1a9805c06)



![{\displaystyle C=\mathbb {E} [B\otimes B]=\mathbb {E} [B\cdot B^{\ast }]={\frac {1}{N}}B\cdot B^{\ast }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/edbe4809b1eaa7822531811761f2beb42a9f090e)










![{\displaystyle g[m]=\sum _{q=1}^{m}{\lambda _{q}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a2d77ec0d0aed1697eb63290ede1171467beeca)
![{\displaystyle g[m=l]\leq 90\%}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2934f8091ff72d70585660f107526daed49b6459)
![{\displaystyle W[p,q]=V[p,q],p=1\dots M,q=1\dots l}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a3a04551425e467e5c59e3354cd9d1f7c9b78c75)

![{\displaystyle s[i]={\sqrt {C[i,i]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2093f7377e953a4e61c0b879f04b9c092b5d25c)

